March 19, 2020 3 min to read

《动物森友会》中拱形地形实现原理

使用opengl来制作一个动森的地图效果吧！

《集合啦！动物森友会》今天发售辣，该游戏以丰富的内容和创新的玩法深深获得猛男们(●ˇ∀ˇ●)的喜爱~辣么，这个拱形的小岛是怎么实现的呢，以下是我的实现思路~~

需要的知识

高等数学中的积分

实现原理

该效果的最终目的就是将一个平面“弯曲”成一个曲面，只要找到合适的曲面函数，将平面的坐标转换成对应曲面的坐标就可以啦~~以下是详细的数学解析：

选定一个曲线函数：这里我们选用的是抛物线，该函数在求积分求导都比较简单，而且满足拱形的原理： y=-bx²(b>0)
设原始的平面上的一点(α,0)，抛物线的最高点为(0,0),则长度L=a-0,我们需要得到在抛物线上距离原点的同样长度为L的位置(α’,β‘)，这样，在该平面上所有的点映射在抛物线上时，任意两点之间的距离与原来未经曲面时的平面是相同的，避免了弯曲导致地面变形的情况出现；
已知(0,α)，求(α’,β’)就是我们第一个目标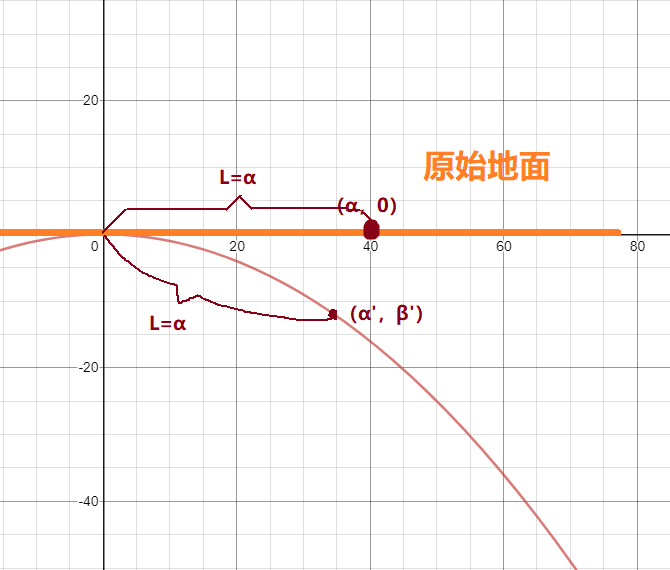：如何求一个曲线的长度？使用曲线积分，我们选用的抛物线是直角坐标方程，其原型公式为: $$\int_α^β\sqrt{1+f`(x)^2} dx$$ $y=-bx^2$求导: $$y=-2bx$$ 代入原公式：$$\int_α^β\sqrt{1+4b^2x^2} dx$$ 解得：
$=x\sqrt{1+4b^2x^2}-\int_α^βx d\sqrt{1+4b^2x^2}$
$=x\sqrt{1+4b^2x^2}-\int_α^β\frac{4b^2x^2}{\sqrt{1+4b^2x^2}}dx$
$=x\sqrt{1+4b^2x^2}-\int_α^β\frac{1+4b^2x^2-1}{\sqrt{1+4b^2x^2}}dx$
$=x\sqrt{1+4b^2x^2}-\int_α^β\sqrt{1+4b^2x^2}dx+\int_α^β \frac{1}{\sqrt{1+4b^2x^2}}dx$
$=x\sqrt{1+4b^2x^2}-\int_α^β\sqrt{1+4b^2x^2}dx+\int_α^β \frac{1}{\sqrt{1+4b^2x^2}}\times \frac{2bx+\sqrt{1+4b^2x^2}}{2bx+\sqrt{1+4b^2x^2}} dx$
$=x\sqrt{1+4b^2x^2}-\int_α^β\sqrt{1+4b^2x^2}dx+\frac{1}{2b}\int_α^β \frac{1}{2bx+\sqrt{1+4b^2x^2}}d(2bx+\sqrt{1+4b^2x^2})$ 所以$\int_α^β \sqrt{1+4b^2x^2}dx = \frac{1}{2}x\sqrt{1+4b^2x^2}+\frac{1}{4b}ln(2bx+\sqrt{1+4b^2x^2})$ 由于求得是(0~β)之间的长度，将x_α=0，x_β=β 带入公式得出长度L：$$L=\frac{1}{2}\sqrt{1+4b^2β^2}+\frac{1}{4b}ln(2bx+\sqrt{1+4b^2β^2})$$ 现：已知L，求长度为L时抛物线上的坐标(α’,β’),其实只要将长度L带入上面的公式，结果就是x坐标的值：$$x_{α'}=\frac{1}{2}\sqrt{1+4b^2L^2}+\frac{1}{4b}ln(2bL+\sqrt{1+4b^2L^2})$$ 将x再带入原始函数中：得出长度为L时映射在抛物线上的点: $(x_{a'},-b(x_{a'})^2)$（对称性）
至此，我们已经通过抛物线上某点到其最高点长度得出该点的实际坐标，完成了平面弧形化的重要一步；
如果就这样直接使用的话，整个场景虽然成为了拱形，但还是会出现一个问题：原本与场景垂直的地方变形后倾斜了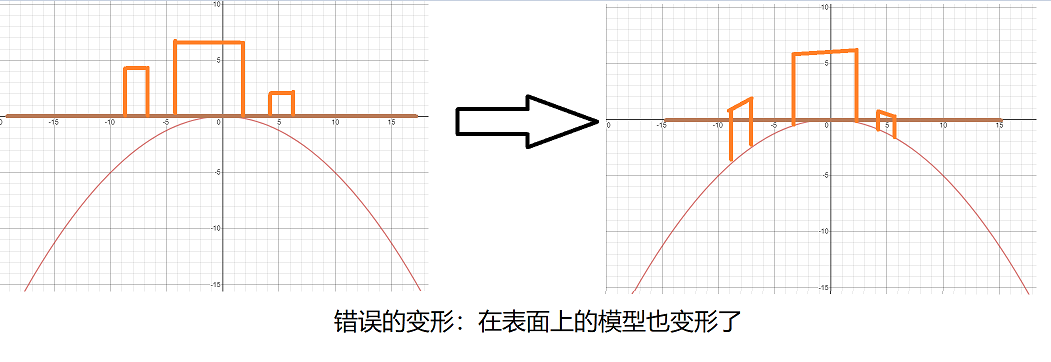：上述的操作我们只针对y=0时的情况将点映射到抛物线上，我们并没有考虑厚度的问题，正确的变形应该如下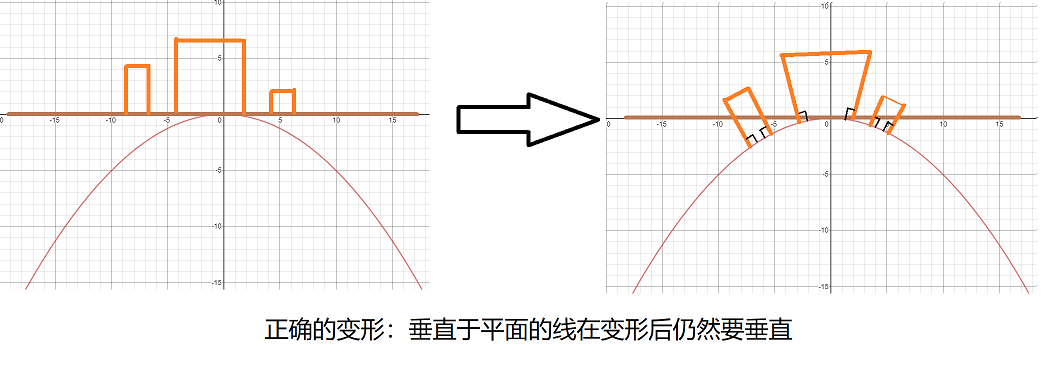：综上，我们需要获得原始点到平面(y=0)的距离$H=y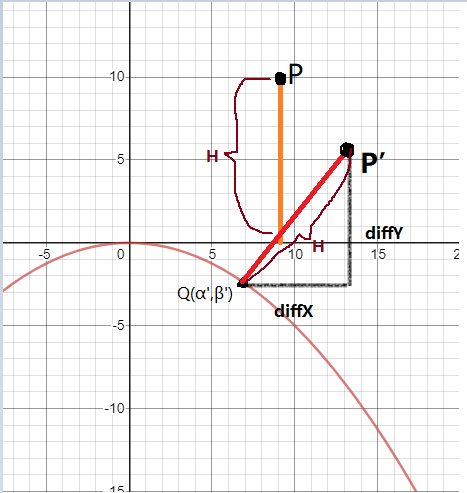$ 在步骤2中我们已经求得了点Q,现需要求得diffY,与diffY来求得最终点P’, 点Q的斜率:

$$S_{Q}=-2bα'$$

线段QP’的斜率：

$$S_{QP'}=-\frac{1}{S_{Q}}$$

$$diffY=\frac{H}{\sqrt{4b^2{Q_X}^2+1}}$$

$$diffX=diffY2b{Q_X}$$

最终点P’的坐标为

$$Q(α'+diffX,β'+diffY)$$

顶点着色器

在shader实现，中我们在平面xz坐标空间进行处理，

#version 330 core

layout(location = 0) in vec3 aPos;
layout(location = 2) in vec2 aTexCoords;

uniform mat4 model;
uniform mat4 projection;
uniform mat4 view;

// y = -bx^2的常数b
uniform float valueB;
// 该函数的原点位置
uniform vec3 centerPoint;

// 光照的变换矩阵
uniform mat4 lightSpaceMatrix;

out vec2 TexCoords;
out	vec3 FragPos;
out vec4 FragPosLightSpace;
void main()
{
	TexCoords = aTexCoords;
	FragPos = vec3(model*vec4(aPos,1.0));
	// 求得该点对于原点的长度；
	float length = FragPos.z-centerPoint.z;
	// 通过长度反向求得对应抛物线上相对x的坐标；
	float relativeZValue = length*sqrt(4*valueB*valueB*length*length+1)/2
	+(log(sqrt(4*length*length*valueB*valueB+1)+2*valueB*length))/4/valueB;

	float relativeYValue = -1*valueB*relativeZValue*relativeZValue;

	// 以上求得了平面点的映射在抛物线的相对坐标：（relativeXValue,relativeYValue）;
	// 法线斜率 为 1/(2*valueB*relativeXValue)，即便是拱形了，也应该物体与平面垂直,所以需要这个垂线
	//求得该点到地面的高度
	float height = FragPos.y-centerPoint.y;
    // 计算diffy和diffz
	float diffy = height/sqrt(4*valueB*valueB*relativeZValue*relativeZValue+1);
	float diffz = diffy*2*valueB*relativeZValue;

    //最终的位置记住加上原点centerPoint的位置
	FragPos = vec3(FragPos.x, relativeYValue+centerPoint.y+diffy, relativeZValue+centerPoint.z+diffz);
	gl_Position = projection *view *vec4(FragPos,1.0);
	//光空间位置
	FragPosLightSpace = lightSpaceMatrix*vec4(FragPos,1.0);

}

我们将函数 $y=-bx^2$的常量b传入valueB中，将函数的最高点位置传入centerPoint(实际上x分量是无意义的)，c++代码如下：

//传入参数
float valueB=0.01;
glm::vec3 centerpoint(0,-2,1);
glUseProgram(shaderID);
// 设置shader的valueB
glUniform1f(glGetUniformLocation(shaderID,"valueB"), valueB);
// 设置shader的centerPoint
glUniform3fv(glGetUniformLocation(shaderID, "centerPoint"), 1, centerpoint);
// 使用该shader绘制场景
drawSence(shaderID)